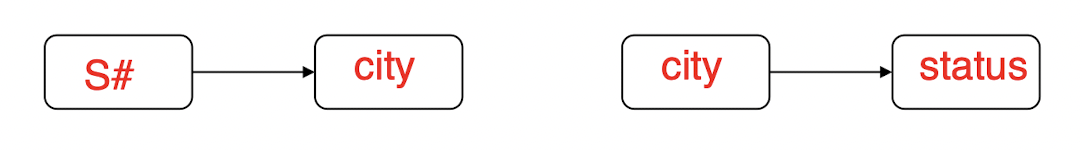Data base system - L5
这篇文章展示了数据库系统的学习记录
Integrity Constraints & Normal Forms
1 Key constraints
-
Superkey of R: A set of attributes SK of R such that no two tuples in any valid relation instance r(R) will have the same value for SK. That is, for any distinct tuples t1 and t2 in r(R), t1[SK] <> t2[SK].
-
Candidate key of R: A “minimal” superkey; that is, a superkey K such that removal of any attribute from K results in a set of attributes that is not a superkey.
-
Primary key of R: choice by the DB designer when there are more than one candidate key
2 Domain/Entity integrity constraints
- No “NULL” value for particular attributes
- Must be “UNIQUENESS”
3 Referential integrity constraints(Foreign key constraints)
- Two relation constraints (single relation above)
- To ensure that a value appears in one relation also appears in another relation.
- Implies “subset dependency” relationship between 2 sets of attributes in 2 tables
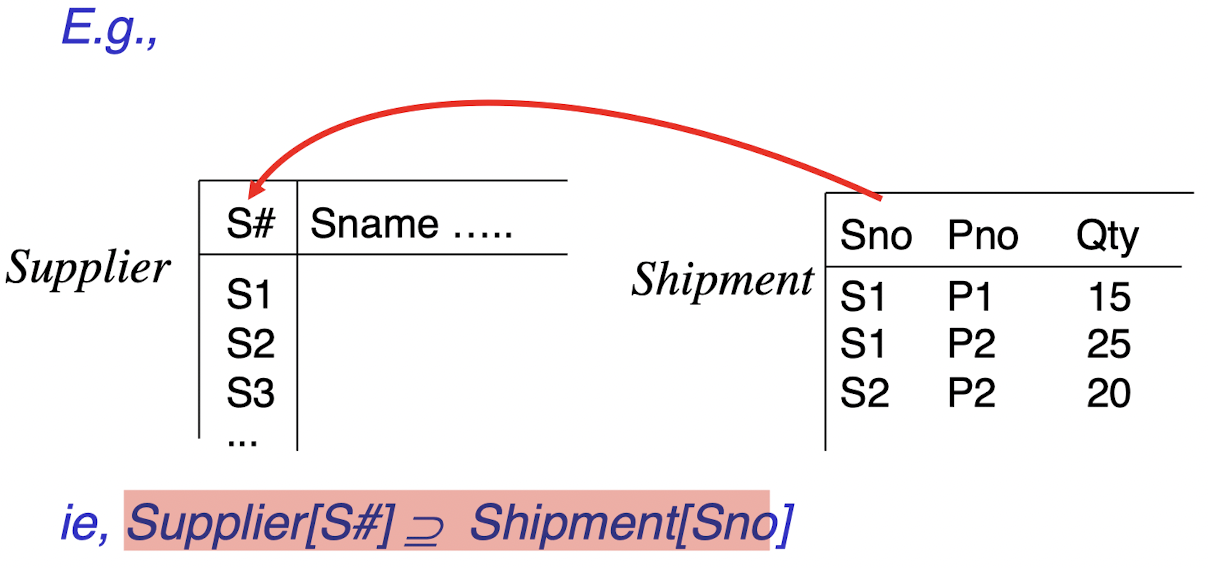
Supplier relation is a foreign table of Shipment
When to check integrity constraints?
- INSERT, DELETE, MODIFY the tuple
4 Functional Dependency
- FD is a particular kind of constraints
- Definition
- R is a relation schema, and $\alpha \subseteq R$, $\beta \subseteq R$, then
- $$\alpha \to \beta$$
- for all pairs of tuples tq and t2 in any legal relation instance r(R), we have
- $$t1[\alpha]=t2[\alpha]\to t1[\beta]=t2[\beta]$$
As a result, FD can be used to identify and find primary key.
4.1 Inference Rules for FDs
-
Given a set of FDs $F$, we can infer additional FDs that hold whenever the FDs in $F$:
- IR1 - Reflexive: If $Y$ is a subset of $X$, then $X\to Y$
- IR2 - Augmentation: If $X\to Y$, then $XZ\to YZ$, ($XZ$ stands for $X \cup Z$)
- IR3 - Transitive: If $X\to Y$ and $Y\to X$, then $X\to Z$
-
Closure of a set $F$ of FDs is the set $F^+$ of all FDs that can be inferred from $F$
-
Equivalence of two sets $F$ and $G$ of FDs
- Every FD in $F$ can be inferred from $G$
- Every FD in $F$ can be inferred from $G$
- Hence, $F$ and $G$ are equivalent if $F^+$ = $G^+$
5 Relational Database Design
5.1 First Normal Form (1NF - 第一范式)
- A relation R is in 1NF if and only if all underlying domians cantain atomic(indivisible) value only
atomic: an attribute can not be decomposed, like, address can be decomposed to province, city, road number, door number, etc.
-
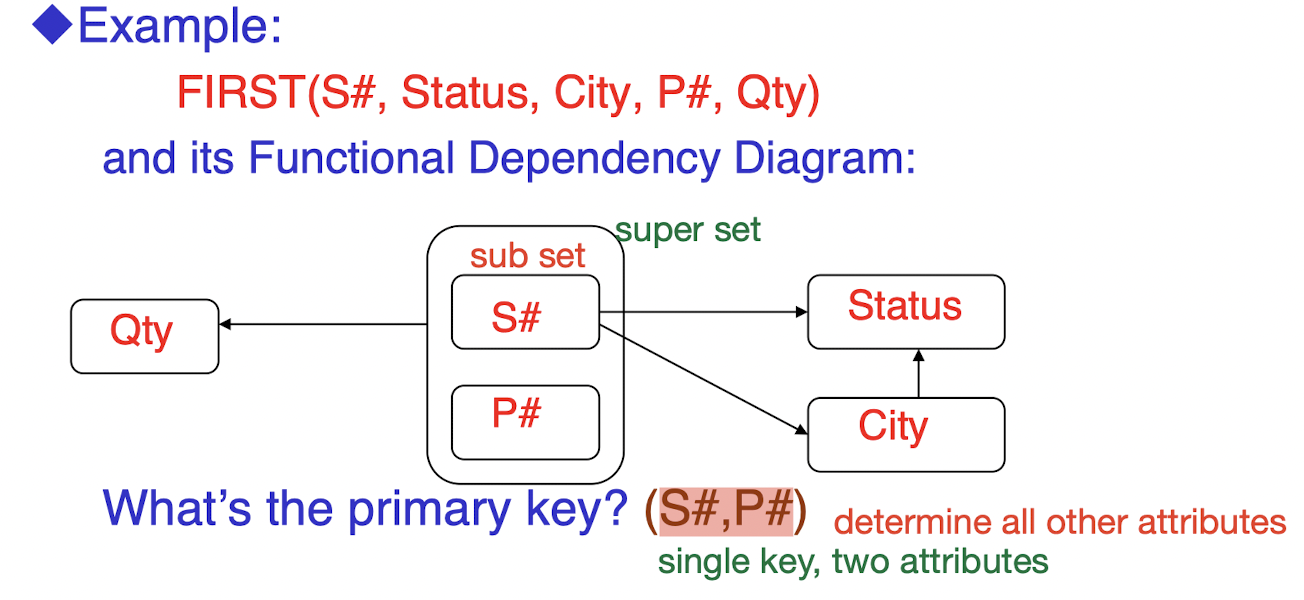
Problem
- Insert Anomalies
- Inability to represent certain information
- Eg, cannot enter “Supplier and City” info until Supplier supplies at least one part(P#)
- Delete Anomalies
- Deleting the “only tuple” for a supplier will destroy all the information about that supplier
- Update Anomalies
- “S# and City” could be redundantly represented for each P#, which may cause potential inconsistency when updating a tuple
- Insert Anomalies
-
Solution(2NF)
- Replace original table by two sub-tables(Normalization)
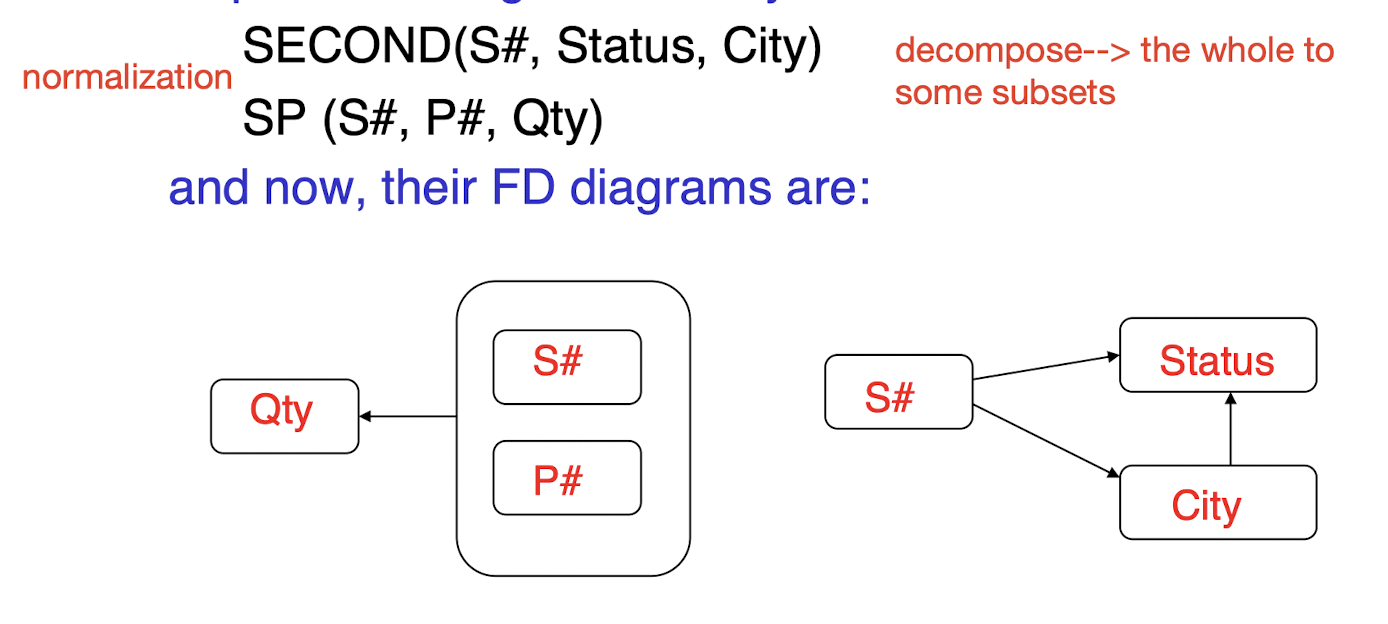
5.2 Second Normal Form (2NF - 第二范式)
- A relation R is in 2NF if amd only if it is in 1NF and every non-key attributes is fully dependent on any candidate/primary key(include that nonprime attribute is transitively dependent on the primary key)
- R(I,C,D,N)
- FD:{I->C, I->D, CD->N, IO->G}
- R is 2NF
- I is a candidate key
- C, D, N are fully (transitively) dependent on I, which can be treated as CD->N <==> I->N
- There is only one type of data stored a particular table, rather a combined-type data.
Both relations are in 2NF in the above case.

- Solution(3NF)
- Replcae second table by two sub-tables
- SC(S#,City)
- CS(City,Status)
- Keep SP(S#,P#,Qty)

- Replcae second table by two sub-tables
5.3 Third Normal Form (3NF - 第三范式)
- A relation R is in 3NF if and only if it is in 2NF and every non-key attribute is non-transitively dependent on any candidate key.
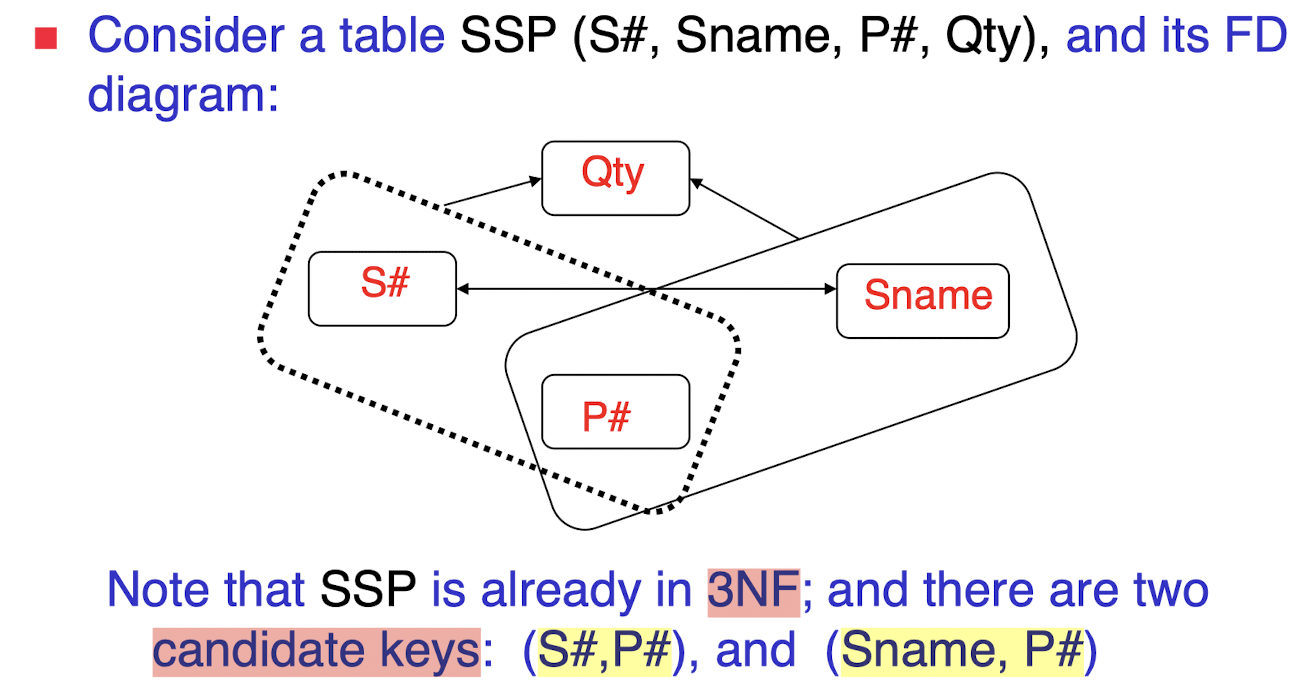
- Some redundancy still exists
- Solution
- Replace original SSP by two sub-tables
- SS(S#,Sname)
- SP(S#,P#,Qty) [or,SP(Sname,P#,Qty)]
5.3 BCNF - BC范式
- A relation R is in BCNF if and only if every determinant (left-hand side of an FD) is a candidate key.
第一范式:1NF是对属性的原子性约束,要求属性具有原子性,不可分解; 第二范式:2NF是对记录的惟一性约束,要求记录有惟一标识,即实体的惟一性; 第三范式:3NF是对字段冗余性的约束,即任何字段不能由其他字段派生出来,它要求字段没有冗余。
学习笔记,仅供参考